回归任务是机器学习中的一个基本问题,其目标是预测一个连续的数值。

- 预测房价
- 预测明天的气温
- 预测股票价格
- 预测用户的消费金额
神经网络,特别是深度神经网络,在处理复杂的、非线性的回归问题时表现出色。
核心思想:为什么神经网络适合回归?
传统的线性回归只能学习数据中的线性关系,而现实世界中的数据关系往往是复杂和非线性的,神经网络的核心优势在于它能够通过多层结构和非线性激活函数来近似任何复杂的函数关系。
一个简单的神经网络可以看作是多个线性变换和非线性激活函数的堆叠:
Output = f(W_n * f(... f(W_2 * f(W_1 * X + b_1)) ... ) + b_n)
通过增加网络的深度和宽度,神经网络可以学习到从输入特征到输出目标值之间极其复杂的映射关系。
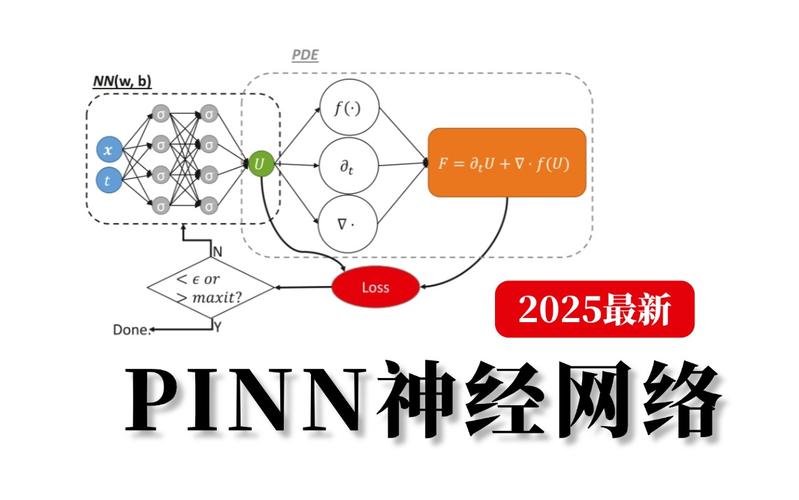
神经网络回归的关键组成部分
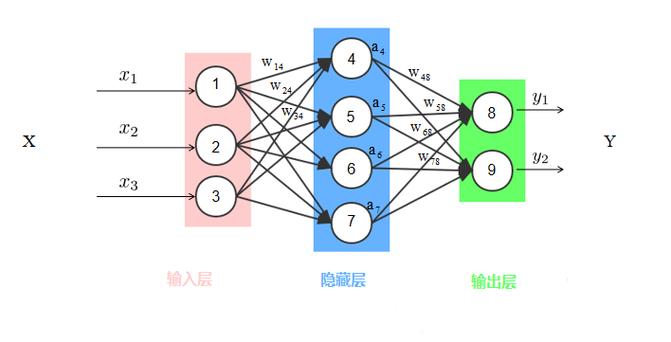
一个用于回归任务的神经网络,在结构上与分类网络非常相似,但在某些关键组件上有区别。
a. 输入层
- 作用:接收原始特征数据。
- 节点数:等于输入特征的个数,如果预测房价的特征有“面积”、“卧室数”、“地理位置”,那么输入层就有3个节点。
b. 隐藏层
- 作用:这是网络的核心,负责从输入数据中提取和组合特征,学习复杂的非线性模式。
- 层数和节点数:这是需要调整的超参数,更多的层和节点可以学习更复杂的模式,但也增加了过拟合的风险和计算成本。
c. 输出层
- 作用:输出最终的预测值。
- 节点数:对于回归任务,输出层通常只有一个节点,这个节点的值就是预测的连续数值。
- 激活函数:这是回归网络与分类网络最重要的区别之一。
- 线性激活函数:这是回归任务最常用的激活函数,它不做任何变换,直接输出加权和,公式为
f(x) = x。 - 为什么用线性? 因为回归问题的目标是一个无界的连续值,如果使用 Sigmoid 或 Tanh 等有界的激活函数,输出会被限制在某个范围内(如 0 到 1),无法预测任意大小的数值。
- 线性激活函数:这是回归任务最常用的激活函数,它不做任何变换,直接输出加权和,公式为
d. 损失函数
- 作用:衡量模型预测值与真实值之间的差距,损失函数的值越小,说明模型预测得越准。
- 常用损失函数:
- 均方误差:这是回归任务最标准、最常用的损失函数,它计算预测值与真实值之差的平方的平均值。
MSE = (1/n) * Σ(y_true - y_pred)²- 优点:对较大的误差给予更高的惩罚,有助于模型快速修正重大错误,数学性质好,易于求导。
- 平均绝对误差:计算预测值与真实值之差的绝对值的平均值。
MAE = (1/n) * Σ|y_true - y_pred|- 优点:对异常值(离群点)不那么敏感,因为平方会放大异常值的影响。
- Huber Loss:结合了MSE和MAE的优点,当误差小于某个阈值δ时,它使用MSE;当误差大于δ时,它使用MAE,这使得它对异常值更鲁棒。
- 均方误差:这是回归任务最标准、最常用的损失函数,它计算预测值与真实值之差的平方的平均值。
e. 优化器
- 作用:根据损失函数计算出的梯度,来更新网络中的权重和偏置,以最小化损失。
- 常用优化器:
- Adam (Adaptive Moment Estimation):目前最流行、最常用的优化器之一,它结合了Momentum和RMSProp的优点,能够自适应地调整学习率,通常表现很好,是大多数任务的默认选择。
- SGD with Momentum:随机梯度下降的改进版本,通过引入动量来加速收敛并减少震荡。
- RMSprop:也常用于处理RNN,能有效处理非平稳目标。
一个简单的神经网络回归模型示例 (使用 Python 和 TensorFlow/Keras)
假设我们要预测一个简单的二次函数 y = 2x² - 3x + 1 加上一些噪声。
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import matplotlib.pyplot as plt
# 1. 生成模拟数据
np.random.seed(42)
X = np.linspace(-1, 1, 200) # 生成200个在[-1, 1]区间的点
# 真实关系 + 高斯噪声
y = 2 * X**2 - 3 * X + 1 + np.random.normal(0, 0.2, size=X.shape)
# 2. 构建模型
# Sequential模型是层的线性堆叠
model = Sequential([
# 输入层:Dense表示全连接层,input_dim指定输入特征维度
# units=64是隐藏层的神经元数量,activation='relu'是常用的非线性激活函数
Dense(units=64, activation='relu', input_dim=1),
# 可以添加更多隐藏层
Dense(units=32, activation='relu'),
# 输出层:units=1因为我们要预测一个数值
# activation='linear'是回归任务的关键!
Dense(units=1, activation='linear')
])
# 3. 编译模型
# 在编译时,我们指定优化器、损失函数和评估指标
model.compile(
optimizer='adam', # 使用Adam优化器
loss='mean_squared_error', # 使用均方误差作为损失函数
metrics=['mean_absolute_error'] # 同时监控平均绝对误差
)
# 打印模型结构
model.summary()
# 4. 训练模型
# epochs训练轮数,batch_size每次训练的样本数,validation_split用于验证
history = model.fit(
X,
y,
epochs=200,
batch_size=32,
validation_split=0.2, # 将20%的数据作为验证集
verbose=1 # 显示训练过程
)
# 5. 评估和预测
# 生成新的数据点进行预测
X_test = np.linspace(-1, 1, 100)
y_pred = model.predict(X_test)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.scatter(X, y, label='Original Data (with noise)')
plt.plot(X_test, y_pred, color='red', linewidth=3, label='Model Prediction')'Neural Network Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()
# 你可以尝试调整网络结构(层数、神经元数)、学习率、损失函数等,观察结果的变化。
面临的挑战与解决方案
a. 过拟合
- 现象:模型在训练数据上表现极好,但在新的、未见过的数据上表现很差,模型“了训练数据的噪声和特定模式,而不是泛化的能力。
- 解决方案:
- 增加数据量:最有效的方法,但往往成本高。
- 正则化:
- L1/L2正则化:在损失函数中加入对权重的惩罚项,限制权重的大小。
- Dropout:在训练过程中,随机“丢弃”(暂时禁用)一部分神经元,强迫网络学习更鲁棒的特征。
- 早停:在训练过程中监控验证集的性能,当验证集的性能不再提升甚至下降时,提前停止训练。
b. 数据预处理
- 归一化/标准化:神经网络对输入数据的尺度非常敏感,如果不同特征的数值范围差异很大(如年龄在0-100,收入在1000-100000),会导致训练困难,通常会将数据缩放到一个较小的范围,如
[0, 1]或均值为0,标准差为1。tf.keras.layers.Normalization层可以方便地实现这一点。
c. 超参数调优
- 需要调整的超参数包括网络层数、每层神经元数、学习率、批次大小、训练轮数等。
- 方法:
- 经验法则:从常见的配置开始尝试(如2-5个隐藏层,每层64-512个神经元)。
- 网格搜索/随机搜索:系统地尝试不同的超参数组合。
- 贝叶斯优化:更智能的超参数搜索方法。
回归 vs. 分类
| 特性 | 神经网络回归 | 神经网络分类 |
|---|---|---|
| 目标 | 预测一个连续值 | 预测一个离散的类别 |
| 输出层节点数 | 1个(预测单个值)或 N 个(预测多个值,如多输出回归) | N 个(N = 类别数) |
| 输出层激活函数 | 线性激活 (Linear) | Softmax (多类), Sigmoid (二类) |
| 常用损失函数 | 均方误差, 平均绝对误差 | 交叉熵 |
神经网络回归是一个功能强大的工具,通过构建合适的网络结构、选择正确的损失函数和优化器,并结合数据预处理和正则化技术,可以有效地解决各种复杂的连续值预测问题。